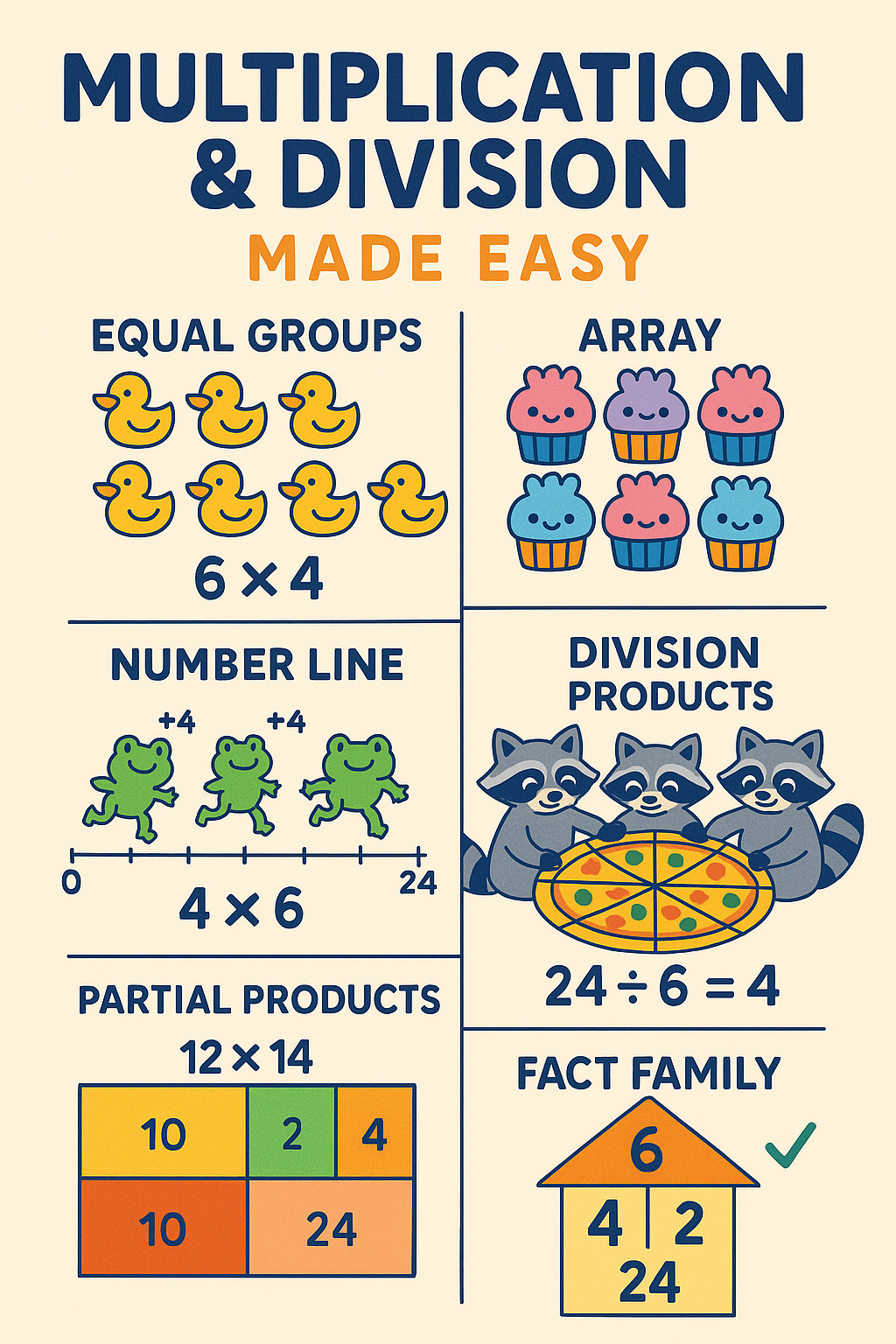
Big idea: multiplication is repeated addition (equal groups), division is fair sharing or grouping. They’re inverse: if 6 × 4 = 24, then 24 ÷ 6 = 4 and 24 ÷ 4 = 6.
1) See the Math: 4 Visual Models
A. Equal Groups (story pictures)
- Multiplication: “6 groups of 4 apples” → 6 × 4 = 24.
- Division (sharing): “24 apples shared among 6 kids” → 24 ÷ 6 = 4 each.
- Division (grouping): “How many groups of 6 fit in 24?” → 24 ÷ 6 = 4 groups.
B. Arrays (rows × columns)
- 3 rows × 5 columns = 15 squares.
- Flip it (commutative): 5 × 3 = 15 too.
C. Number Line (skip-count jumps)
- 4 × 6 = six jumps of +4 (or four jumps of +6).
- 24 ÷ 6 = “How many +6 jumps to reach 24?” → 4 jumps.
D. Area Model (rectangle)
- 12 × 14 = (10 + 2)(10 + 4)
= (10×10) + (10×4) + (2×10) + (2×4)
= 100 + 40 + 20 + 8 = 168.
2) Core Facts & Friendly Anchors
Memorize smart, not hard. Use anchors you already know:
- 0s & 1s: 0×n = 0, 1×n = n.
- 2s (double): 2×7 = 14 → double again for 4s: 4×7 = 28.
- 5s: half of 10s (5×8 = half of 80 = 40).
- 10s: add a zero (10×9 = 90).
- 9s trick (to ×9): 9×7 → 63 (digits sum to 9; or 7th multiple is 63).
- Commutative: 3×8 = 8×3 (learn one, get two).
- Squares: 3×3, 4×4, … are helpful “landmarks”.
Fact families: If 7×6=42, then 6×7=42, 42÷7=6, 42÷6=7.
3) Multiplication Strategies (from simple to strong)
A. Skip Count / Groups
- 6 × 4 → 6 groups of 4: 4, 8, 12, 16, 20, 24.
B. Break Apart (Distributive Property)
- 7 × 8 = (7 × 5) + (7 × 3) = 35 + 21 = 56.
- 13 × 6 = (10 × 6) + (3 × 6) = 60 + 18 = 78.
C. Doubling & Halving (keep the product the same)
- 25 × 12 → (25 × 3) × 4 = 75 × 4 = 300.
- Or half one factor, double the other: 50 × 6 = 300.
D. Area / Partial Products (2-digit × 2-digit)
- 34 × 27
= (30 + 4)(20 + 7)
= 30×20 600 + 30×7 210 + 4×20 80 + 4×7 28
= 918.
E. Standard Algorithm (when ready)
Line up by place value, multiply ones, then tens, add partial rows.
4) Division Strategies (two meanings)
Meaning 1: Sharing (result is size of each share)
- 24 ÷ 6 = 4 each (24 things into 6 equal groups).
Meaning 2: Grouping (result is number of groups)
- 24 ÷ 6 = 4 groups (how many 6s fit in 24).
A. Think “What times what?”
- 56 ÷ 8 → “8 × ? = 56” → 7 (fact family thinking).
B. Repeated Subtraction / Number Line
- 42 ÷ 7 → subtract 7s: 42, 35, 28, 21, 14, 7, 0 → 6 jumps.
C. Partial Quotients (friendly chunks)
- 196 ÷ 14
- Take 10 groups of 14 (140). Remainder 56.
- Take 4 groups of 14 (56). Remainder 0.
- Total groups = 10 + 4 = 14.
D. Interpreting Remainders
- 53 ÷ 8 = 6 remainder 5 (6 R5).
- In money or measurement, convert the remainder:
- 53 cookies into bags of 8 = 6 full bags, 5 left.
- 53 minutes into blocks of 8 minutes ≈ 6 blocks, 5 minutes extra.
E. Divisibility Quick Checks
- 2: even last digit.
- 3: digit sum divisible by 3.
- 5: ends in 0 or 5.
- 10: ends in 0.
- (Useful to test factors before dividing.)
5) Word-Problem Templates
Multiplication (equal groups):
- “There are 7 tables with 6 chairs each. How many chairs?” → 7 × 6.
Multiplication (array/area):
- “A garden is 9 m by 4 m. What’s the area?” → 9 × 4.
Division (sharing):
- “48 stickers shared among 6 kids. How many each?” → 48 ÷ 6.
Division (grouping):
- “I have 48 stickers. If 6 go in a pack, how many packs?” → 48 ÷ 6.
Two-step mix:
- “3 boxes hold 8 notebooks each. 6 students share them equally. How many per student?”
- 3 × 8 = 24 total; 24 ÷ 6 = 4 each.
6) Check Your Work (inverse + estimate)
- Use inverse: If 39 × 6 = 234, then 234 ÷ 6 should be 39.
- Estimate: 48 × 21 ≈ 50 × 20 = 1000 (a quick reasonableness check).
7) Common Mistakes & Quick Fixes
- Order confusion in division: 24 ÷ 6 ≠ 6 ÷ 24.
- Fix: say it both ways—“24 split into 6 equal groups.”
- Dropping a partial product zero:
- Fix: place-value layout; write each row under tens/hundreds.
- Remainders forgotten:
- Fix: circle the remainder and interpret it (“left over,” “round up,” or convert).
8) Practice (with answers)
A. Facts
- 6 × 7 = __
- 9 × 8 = __
- 54 ÷ 9 = __
- 63 ÷ 7 = __
Answers: 42, 72, 6, 9
B. Friendly numbers
- 5 × 14 = __ (think 10s)
- 25 × 12 = __ (double/half)
Answers: 70, 300
C. Distributive
- 7 × 16 = 7×10 + 7×6 = __
- 18 × 24 = (20−2)×24 = 20×24 − 2×24 = __
Answers: 70 + 42 = 112; 480 − 48 = 432
D. Area / partial products
- 23 × 15 = (20+3)(10+5) = __
Answer: 200 + 100 + 30 + 15 = 345
E. Division—partial quotients
- 252 ÷ 12 = __
One way: 10×12=120 (remainder 132), 10×12=120 (rem 12), 1×12=12 → 21
F. Remainders
- 53 ÷ 8 = __
Answer: 6 R5
9) Mini Cheat Sheet
- Multiply: groups, arrays, area, skip count; use distributive; double/half.
- Divide: sharing or grouping; think multiplication facts; partial quotients.
- Properties: commutative (× only), associative (× only), distributive (× over +).
- Check: inverse & estimate.