The Big Idea (in one minute)

• Addition joins quantities: part + part = whole.
• Subtraction finds what’s left, the distance between numbers, or a missing part: whole − part = part.
• They are inverse operations—you can check addition by subtracting, and check subtraction by adding.

Everything in this guide reinforces three mental models:

1. Number lines (moving forward/backward a distance),
2. Base-ten blocks (tens and ones you can regroup), and
3. Part–part–whole bars (what goes with what to make the whole).

We’ll move from hands-on to symbolic, so learners always know why a step works before they memorize how.

---

Core Models and What They Teach

1) Number Line (counting and distance)

A number line turns addition into forward “jumps” and subtraction into backward “jumps.”

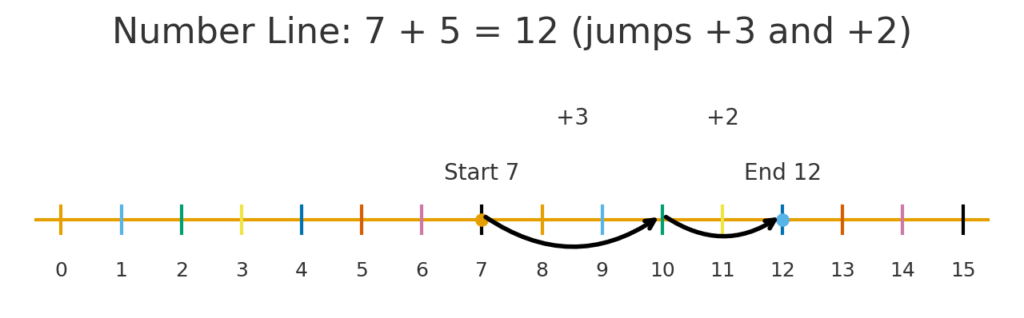
• Illustration 1: 7 + 5 = 12 using jumps of +3 and +2.
  

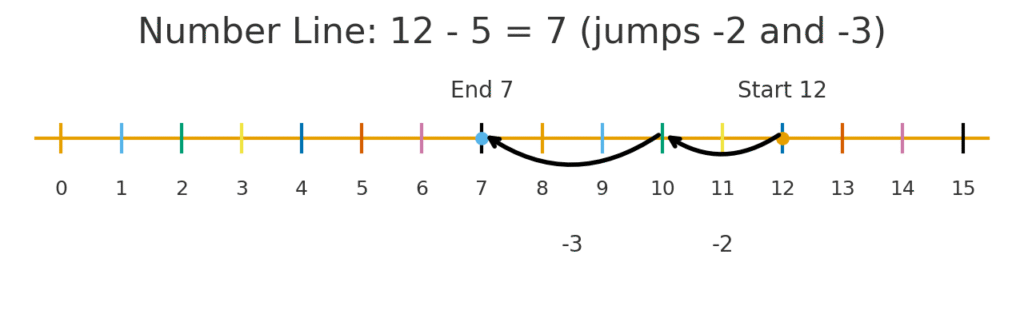
• Illustration 2: 12 − 5 = 7 as jumps −2 and −3.
  
• Why it helps:
• Builds magnitude sense—5 is a distance, not just a symbol.
• Naturally leads to counting on (addition) and counting back/up (subtraction).
• Prepares students for absolute value and negative numbers later.

2) Base-Ten Blocks (place value and regrouping)

Think of a ten rod as a bundle of 10 ones. You can regroup 10 ones → 1 ten, or unbundle 1 ten → 10 ones.

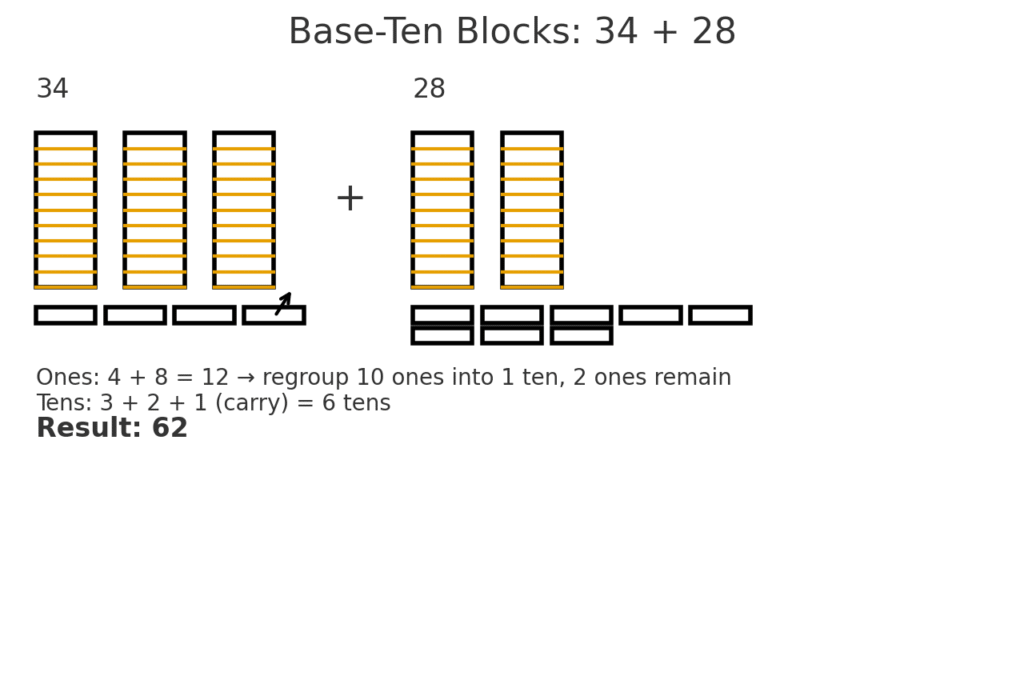
• Illustration 3: 34 + 28 = 62 using ones-then-tens, with a carry.

Why it helps:

• Makes carrying (addition) and borrowing (subtraction) tangible.
• Reduces fear around “across the zero” problems (like 402 − 187) because you can see the trades.

3) Part–Part–Whole Bars (missing addend thinking)

• Illustration 4: 17 = 9 + ? (So ? = 17 − 9).
  See: Bar model 17 = 9 + ?

Why it helps:

• Shows subtraction as finding a missing part, not just “take away.”
• Converts word problems into visual chunks you can reason about.

4) Fact Families (the four related equations)

• Illustration 5: 3, 5, and 8 form a family:
  3 + 5 = 8, 5 + 3 = 8, 8 − 3 = 5, 8 − 5 = 3.
  See: Fact family triangle

Why it helps:

• Encodes the inverse relationship between addition and subtraction.
• Cuts memorization in half—know one fact, get the other three for free.

---

Addition—From Counting to Algorithms

A. Early strategies (K–1)

1. Count all: Put out counters for both parts and count everything.
2. Count on: Start at the larger addend and count up the smaller.
   • Example: 7 + 5 → “7… 8, 9, 10, 11, 12.”
3. Make ten: Decompose to hit a friendly ten.
   • 8 + 5 = 8 + (2 + 3) = (8 + 2) + 3 = 10 + 3 = 13.
4. Doubles & near doubles:
   • Doubles you know (6 + 6 = 12).
   • Near doubles (6 + 7 = 6 + 6 + 1 = 13).

Why these matter: They are brain-efficient. “Make ten” and “near doubles” are the engine of mental addition to 20.

B. Place value addition (2–3 digit)

Ones then tens (base-ten language)

Example: 34 + 28

• Ones: 4 + 8 = 12 → put down 2, carry 1 ten.
• Tens: 3 tens + 2 tens + 1 ten (carry) = 6 tens.
• Total = 62.
  (See the base-ten illustration.)

Standard vertical algorithm (what you see in textbooks)

34

+ 28

62

• Align place values.
• Add ones (regroup if ≥10).
• Add tens (include the carry).

Friendly-number compensation

• 34 + 28 → bump 28 up to 30 (add 2), but then subtract 2:
  34 + 30 − 2 = 64 − 2 = 62.
• Great for mental math and estimation checks.

C. Properties that make addition work

• Commutative: a + b = b + a (order doesn’t change the sum).
• Associative: (a + b) + c = a + (b + c) (grouping doesn’t change the sum).
• Identity: a + 0 = a.

Teaching move: Put three addends up and have students rearrange to make a ten first:
7 + 9 + 3 = (7 + 3) + 9 = 10 + 9 = 19.

D. Multi-digit with regrouping (3 or more digits)

568

– 297

865 (work it out)

Walkthrough:

1. Ones: 8 + 7 = 15 → write 5, carry 1.
2. Tens: 6 + 9 + 1 = 16 → write 6, carry 1.
3. Hundreds: 5 + 2 + 1 = 8 → write 8.
   Answer: 865.

Common pitfall: Carry written in the wrong column. Fix with color-coding carries (or simply circle them in pencil and erase after).

E. Mental addition beyond 20

• Break-apart: 47 + 36 = (40 + 30) + (7 + 6) = 70 + 13 = 83.
• Constant difference (compensation): 47 + 36 → (47 + 3) + (36 − 3) = 50 + 33 = 83.
• Chunking: 385 + 417 → (385 + 400) + 17 = 785 + 17 = 802.

---

Subtraction—Three Meanings, One Operation

Subtraction can be understood as:

1. Take away: remove a set.
2. Difference: distance on a number line.
3. Missing addend: what completes the whole.

Switching between meanings makes students flexible and less likely to get stuck.

A. Early strategies (K–1)

1. Count back: 12 − 3 → “12… 11, 10, 9.”
2. Count up (distance): From 9 up to 12 (3 steps).
3. Use a known fact family: If 5 + 7 = 12, then 12 − 7 = 5 and 12 − 5 = 7.
4. Make ten then subtract: 13 − 8 = (13 − 3) − 5 = 10 − 5 = 5.

Pro tip: For many learners, counting up is easier than counting back—it’s the same cognitive move as addition, just targeted at the gap.

B. Place value subtraction (with and without regrouping)

Without regrouping

Example: 562 − 241

• Ones: 2 − 1 = 1
• Tens: 6 − 4 = 2
• Hundreds: 5 − 2 = 3
  Answer: 321.

With regrouping (borrowing)

Example: 402 − 187

Base-ten story: “We have 4 hundreds, 0 tens, 2 ones. We need 7 ones; borrow 1 ten… but there are no tens to borrow. Borrow 1 hundred, convert to 10 tens; then take 1 ten from those to convert to 10 ones.”

Symbolically:

402

– 187

• Borrow from hundreds: 4→3 hundreds, tens become 10.
• Borrow from tens: 10→9 tens, ones become 12.
• Ones: 12 − 7 = 5
• Tens: 9 − 8 = 1
• Hundreds: 3 − 1 = 2
  Answer: 215.

Why slow down here: Most errors happen because students lose track of the trades. Say each trade out loud like a recipe:
“Trade 1 hundred → 10 tens; trade 1 ten → 10 ones.”

C. Subtraction by adding (count-up method)

Especially strong for across-decade numbers.

Example: 405 − 397

Count up from 397: +3 → 400, +5 → 405, total 8.
This beats juggling multiple borrows and mirrors real-world difference thinking.

D. Compensation (constant difference)

Example: 52 − 19 → add 1 to both numbers: 53 − 20 = 33 (same difference, easier arithmetic).
Use when a subtrahend is just below a “friendly” number.

E. Mixed strategy toolbox

• Make tens & hundreds (13 − 6 → (10 − 6) + 3).
• Break-apart (83 − 27 → (80 − 20) + (3 − 7) = 60 − 4 = 56).
• Bar model for missing addend (17 = 9 + ? → ? = 8). See the bar illustration.

---

Word Problems (and how to actually solve them)

Template 1: Join/Separate

• Join: “A jar has 12 marbles. Sam adds 7. How many now?” → 12 + 7.
• Separate: “A jar has 19 marbles. Sam gives away 8. How many left?” → 19 − 8.

Template 2: Compare (difference)

• “Ana read 24 pages, Leo read 17. How many more pages did Ana read?” → 24 − 17.

Template 3: Missing part

• “A sandwich costs $9. I have $4. How much more do I need?” → ? + 4 = 9 → 9 − 4.

3-step routine (bar model ready):

1. Draw a part–part–whole bar.
2. Label what you know.
3. Write the equation that matches the bar; solve.

---

Checking Work (because accuracy matters)

• Inverse check: For 47 + 36 = 83, verify 83 − 47 = 36 (or 83 − 36 = 47).
• Estimate: Round to tens/hundreds and see if your exact answer is reasonable.
• Digital sum sense (sanity check): If you add 1 to one addend and subtract 1 from the other, the sum stays the same; handy for mental checks.

---

Common Misconceptions (and quick fixes)

1. Stacking without alignment → Misplaced ones/tens/hundreds.
   • Fix: Use graph paper or lightly draw columns.
2. Forgetting the carry/borrow in later columns.
   • Fix: Circle the carry, cross it out once used. Say trades out loud.
3. Subtraction “bigger from smaller” reversal (writing 3 − 8 instead of 13 − 8 after a borrow).
   • Fix: Track the new digit after borrowing before subtracting.
4. Over-inking on number lines (counting extra).
   • Fix: Label each hop with its size and stop on the destination tick, not beyond it.

---

Practice Sets (with answers)

A. Fluency within 20

1. 8 + 7 =
2. 9 + 6 =
3. 12 − 5 =
4. 14 − 9 =
5. 6 + 6 =
6. 13 − 8 =
7. 10 − 7 =
8. 7 + 5 =
9. 15 − 7 =
10. 9 + 4 =

Answers: 1)15 2)15 3)7 4)5 5)12 6)5 7)3 8)12 9)8 10)13

B. Place value (two-digit)

1. 34 + 28 =
2. 56 − 19 =
3. 47 + 36 =
4. 63 − 27 =
5. 80 − 45 =

Answers: 1)62 2)37 3)83 4)36 5)35

C. With regrouping (three-digit)

1. 568 + 297 =
2. 402 − 187 =
3. 735 − 468 =
4. 416 + 287 =
5. 900 − 456 =

Answers: 1)865 2)215 3)267 4)703 5)444

D. Number line / distance

1. Distance between 27 and 34 =
2. 52 − 48 by counting up =
3. 105 − 98 by counting up =

Answers: 1)7 2)4 3)7

E. Word problems

1. You have 18 stickers and get 7 more. Then you give away 9. How many now?
2. A bus holds 48 people. 29 riders are on it. How many empty seats?
3. A runner’s total is 10 km across two days. Day 1 was 4 km. How many on Day 2?

Answers: 1)18 + 7 − 9 = 16 2)48 − 29 = 19 3)10 − 4 = 6

---

Games & Routines That Build Skill (5–10 minutes)

• Make-Ten War: Draw two cards each, make the closest to 10; explain your strategy.
• Target 100: Add three numbers that sum close to 100; talk through round-and-adjust moves.
• Race to Zero (subtraction): Start at 50; roll a die and subtract; first to 0 wins—must explain each borrow aloud.
• Hopscotch Line: Chalk a line 0–20; call “+3, −2” sequences kids hop out.

---

For Parents & Teachers

• Sequence: Start with concrete (counters/blocks), move to representational (drawings, bars, number lines), finish with abstract (equations).
• Say the math: Students should narrate trades: “I trade 1 ten for 10 ones.” Language cements understanding.
• Short, frequent practice beats marathons. Five quality problems with discussion > twenty silent items.
• Celebrate strategies: There’s more than one right way. Ask: “Why did that work?” “Could there be a faster way?”

Mini Reference—Strategies at a Glance

Addition

• Count on; make ten; doubles/near doubles; break-apart; compensation; vertical algorithm with regrouping.

Subtraction

• Count back; count up (difference); make ten; compensation; break-apart; vertical algorithm with borrowing.

Connections

• Fact families; inverse check; bar models; number lines; base-ten regrouping.

---

Wrap-Up

Addition and subtraction are two sides of the same coin: joining and separating, whole and parts, forward and backward on a line. When students can see the math (with blocks, bars, and lines) and say the logic (trades, hops, and checks), procedures stop feeling like magic tricks and start feeling inevitable.